Week 1
| Class | C4W1 |
|---|---|
| Created | |
| Materials | |
| Property | |
| Reviewed | |
| Type |
Convolutional Neural Networks
Computer Vision
Computer vision is one of the areas that's been advancing rapidly thanks to deep learning. Deep learning computer vision is now helping self-driving cars figure out where the other cars and pedestrians around so to avoid them.
Some computer vision problems deep learning can help fix:
- Image classification
- Object detection (multiple bounding boxes)
- Neural Style Transfer
Challenges of computer vision:
- Input data can be large to handle
- Computations resources
Edge Detection Example
The convolution operation is one of the fundamental building blocks of a convolutional neural network. Using edge detection as the motivating example in image below, we see how the convolution operation works.
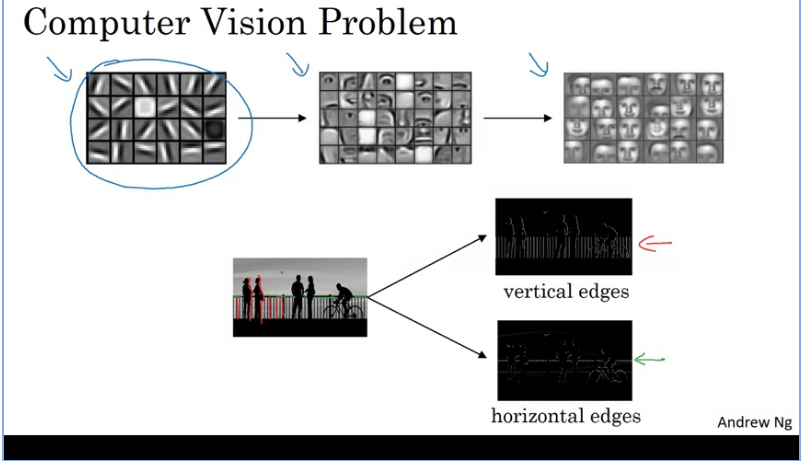
Looking at the image about we can create a nn such that:
- Layer 1: Detect edges
- Layer 2: Cause of objects
- Later layer: Detect people's faces
Given an image for a computer to figure out what's in the image,
- The first thing to do would be to detect vertical edges in the image.
- Detect horizontal edges in the image.
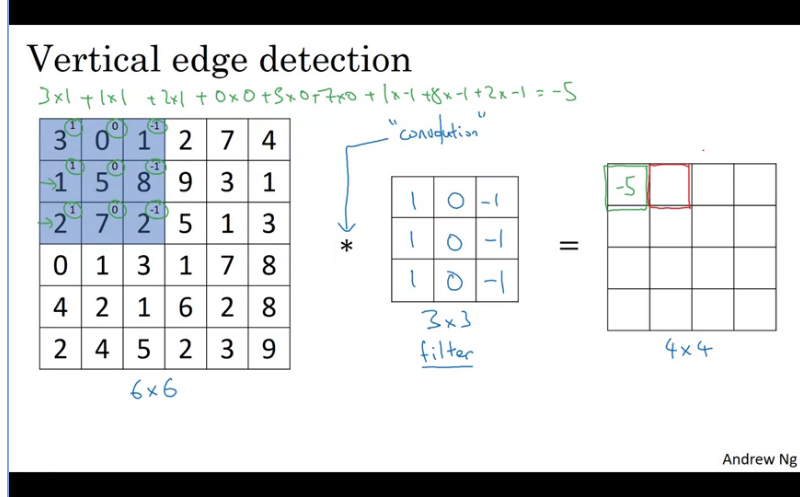
How to detect edges in an image
Iteratively:
- Construct a 3x3 filter/kernel
- Convolve the 6x6 matrics with the kernel
These layers slide (convolve) over the input data, generating a number of 'feature maps' than can subsequently be used to detect certain patterns in the data. This is achieve by element-wise multiplications between the slice of the input data and the filter/kernel which is currenty hovering over.
- Output will be a 4x4 matrics.
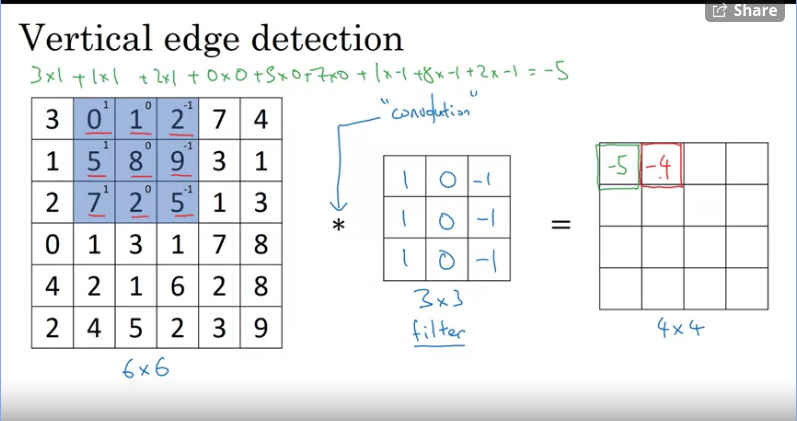
Continue to the next matrics...and so on...
This turns out to be a vertical edge detector in the end.
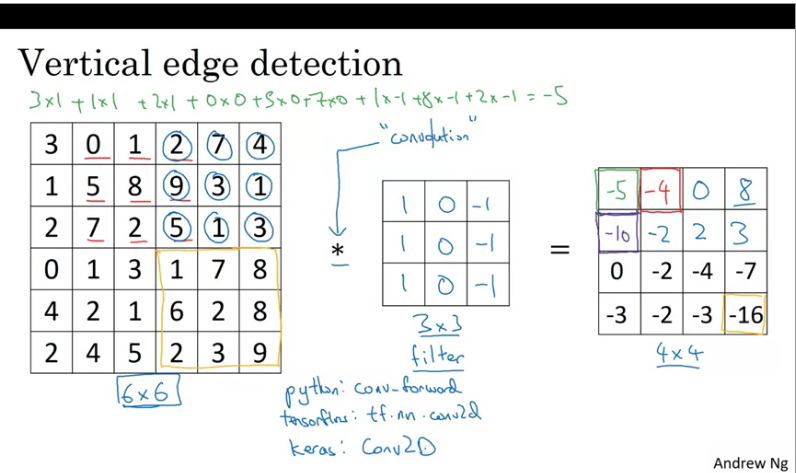
Now let's look at another example:
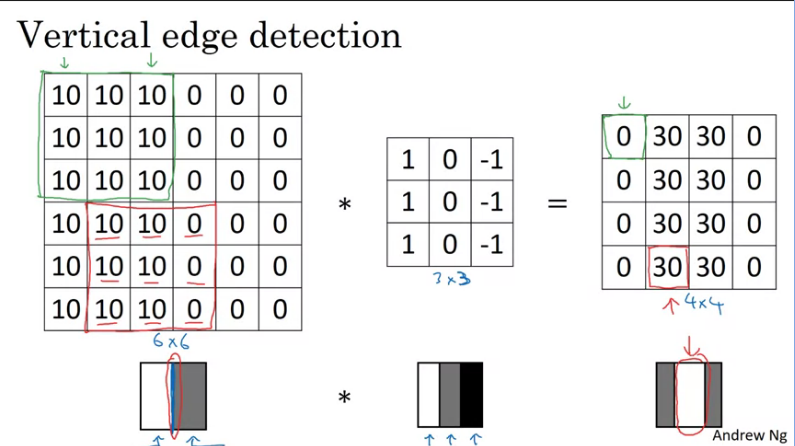
From the image above the detected edge seems to be in the middle and the bright region on the output images tells us that it found a vertical edge in the middle of the image on the left. The reason why it is thick is because we are dealing with very small matrices, if it was a large image the output would be different.
One intuition to take away from the vertical edge detection is that a vertical edge is a 3x3 region since we are using a 3x3 filter where there are bright pixels on the left and dark pixels on the right.
More Edge Detection
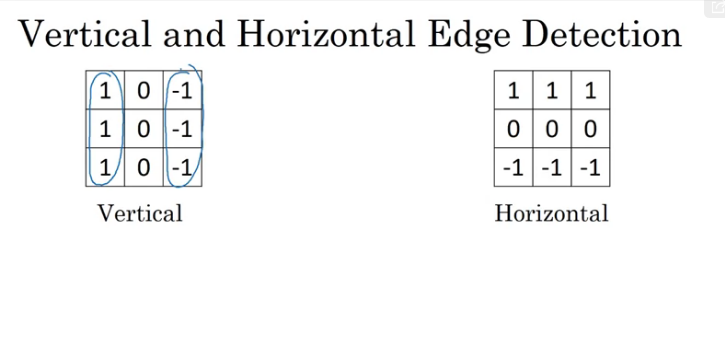
A vertical edge detector according to the filter is a 3x3 region where the pixels are relatively bright on the left part and relatively dark on the right part. Similarly, a horizontal edge detector would be 3x3 region where the pixels are relatively bright on top and dark in the botton row.
In summary, different filters allows us to find vertical and horizontal edges and it turns out that the 3x3 vertical edge detection filter is one possible choice.
Learning to detect edges with different filters:
- Sobel filter: Advantage is that it puts a little bit more weight to the central row and makes it more robust
- Scharr filter: This filter has different properties and it's mainly used for vertical edge detection.
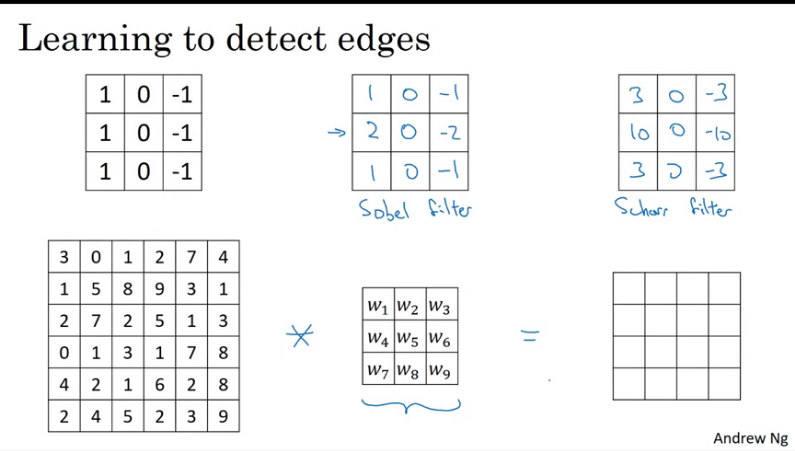
With the rise of deep learning one of the things we learned is that when you really want to detect edges in a complicated image, you probably do not need to hardcode those numbers instead you can learn them and treat the nine numbers of the matrix as parameters, which can be learned using back propagation.
Padding
In order to build deep neural networks one modification to the basic convolutional operation that you need is to use padding.
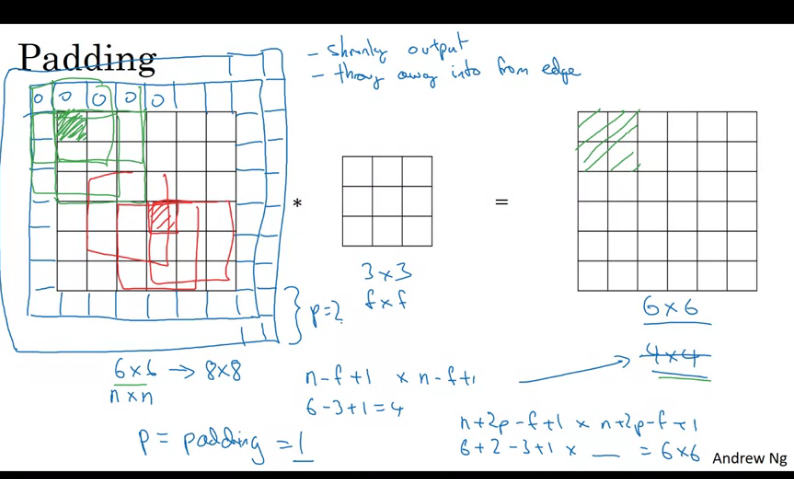
In the image above, if you convolve an input image with dimensions with a kernel of dimensions the output dimensions will be
Disadvantages to convolving out input image with a kernel are:
- Your images shrinks everytime you convolve it
- Certain pixels (especially in the middle of the image) become overlapped when convolving, you end up throwing a lot of information from the edges of the image.
Sometimes you don't want your input to become smaller, this can be achieved with the 'padding mechanism'.
How to fix the above issues:
- Pad the image with an padding around the image such that now you have input image, this ensures that after convolving you retain the original size of the image.
This method is usually referred to as Zero Padding, when applying zeros around the image.
Useful resource: https://www.machinecurve.com/index.php/2020/02/07/what-is-padding-in-a-neural-network/
How much to pad? There's 2 common choices when it comes to padding:

Note: It is common in computer vision to use a kernel size odd value.
Strided Convolutions
Strided convolutions is another piece of the basic building block of convolutions as used in Convolutional Neural Networks. As shown in the example below. Suppose you want to convolve this image with this filter/kernel, except that instead of doing the usual way, we are going to do it with a stride of 2. What that means is you take the element-wise product as usual in this upper left region and then multiply and add and that gives you 91. But then instead of stepping the blue box over by one step, we are going to step over by two steps. So, we are going to make it hop over two steps as shown.
Notice how the upper left hand corner has gone from this start to this start, jumping over one position. And then you do the usual element Y's product and summing it turns out 100. so on...
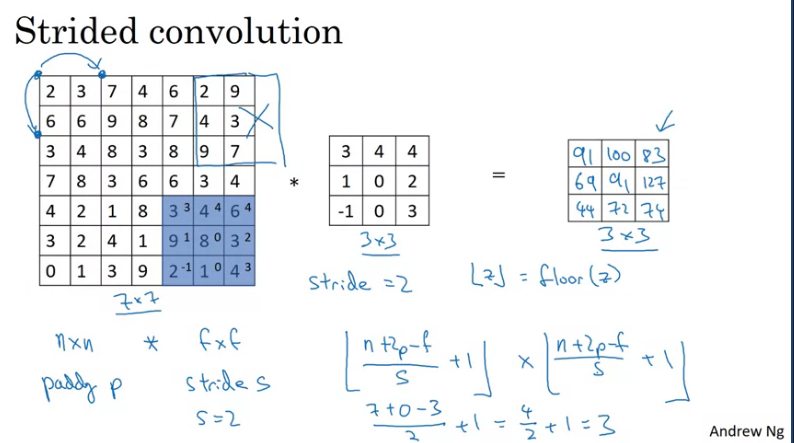
Note: If the value of is a float then you take the floor of that value: np.floor(f)
In summary:

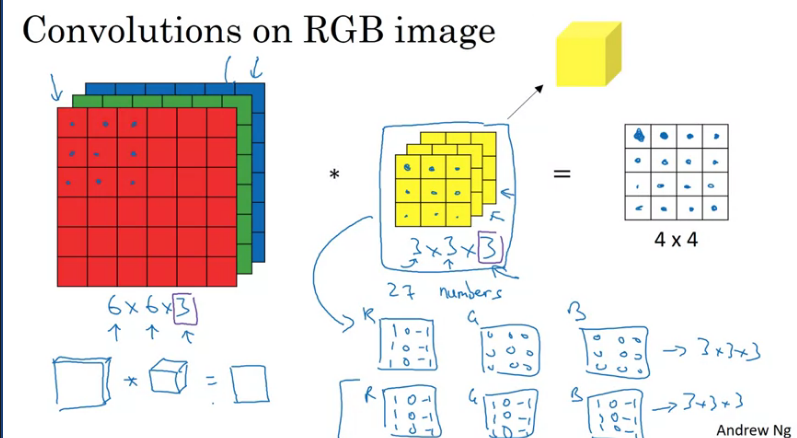
Convolutions Over Volume
Suppose you want to detect features on an RGB image, in order to detect them you would convolve the image with a 3 channel/depth filter. The number of channels in the image should match the filters channel.
The benefit of using a 3 channel filter is that you could filter specific colors of the RGB image, In the example below you could set the kernel to only detect vertical edges only in the Red channel/depth by setting the Green and Blue to zero.
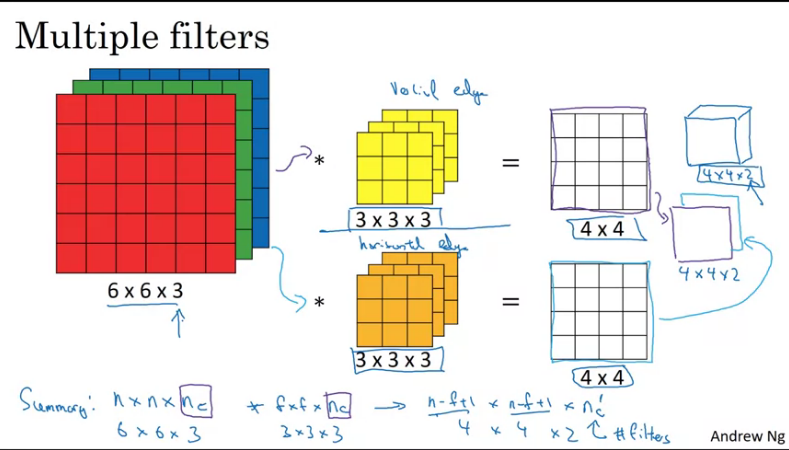
Suppose you want to have multiple filters in an image, you could similarly apply the above but instead now your output will have x channel(s) depending on the number of filters used.
One Layer of a Convolutional Network
Similarly, when convoling convnets we follow the same approach as shown above but instead now we treat everything as convnets.
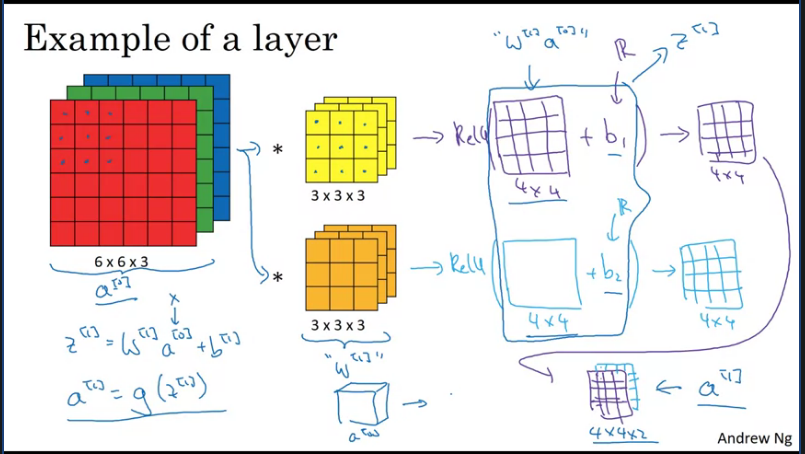
Summary of notation

Simple Convolutional Network Example

Suppose you have an image that you want to do image classification/recognition. Where you take an input image X and decide if image contains a cat or not.
You could build a simple ConvNet as shown above. Suppose the image dims are and say we convolve this input image with a 3 layered 1 strided 10 filters with no padding in order to detect features.
The dims of the activations in the next layer of the nn will be , 10 resulting from the number of filters from the previous kernel used.
Suppose you want to pass it through another filter ( filter) and maybe with no padding and 20 filters. The output of that will be another volumed nn which will be a , due to the use of 2 strides the dimensions shrunk much faster from to .
If we apply another filter before flattening the results in order to get our softmax probabilities we could end up with a volume with 1960 values. By simply using a filter a stride of 2 and 40 filters with no padding.
This means that we went from an RGB image of to features of the images which will be flattened to 1960 units. What's left is to feed this units into a logistic regression or softmax unit.
Types of layer in a convolutional network:
- Convoltion (Conv)
- Pooling (Pool)
- Fully connected (FC)
Pooling Layers
Other than convolutional layers, ConvNets often also use pooling layers to reduce the size of the representation, to speed the computation, as well as make some of the features that detects a bit more robust
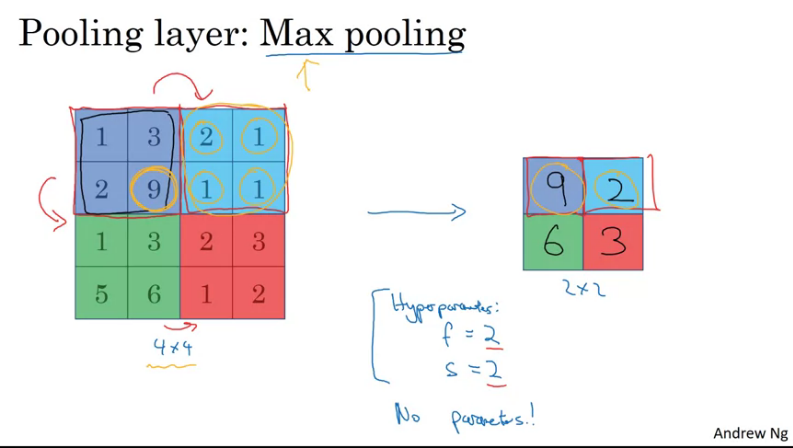
Suppose you have a 4x4 input and want to apply a pooling called max pooling. Max pooling is the process of reducing the size of an input image by simmarizing regions, values are converted into a single value by taking the maximum value from among them.
So we would need to take the 4*4 input and break it into different regions, then take the max of each shaded region into its corresponding region on the right (2*2 region).
This is as if you are applying a 2 layer filter with a stride of 2.
The intuition behind what's maxpooling is doing, if you think of this 4*4 region as some set of features, the activations in some later of the nn. Then a large number, means a particular feature was detected. So that the max operation does is as long as the features is detected anywhere in one of the quadrants, it then remains preserved in the output of max pooling. In short, if these features are detected anywhere in this filter, then keep a high number and if not detected then feature does not exist.
One interesting property of max pooling is that it has a set of hyperparametes but it has no parameters to learn i.e nothing for gradient descent to learn.
Resource:
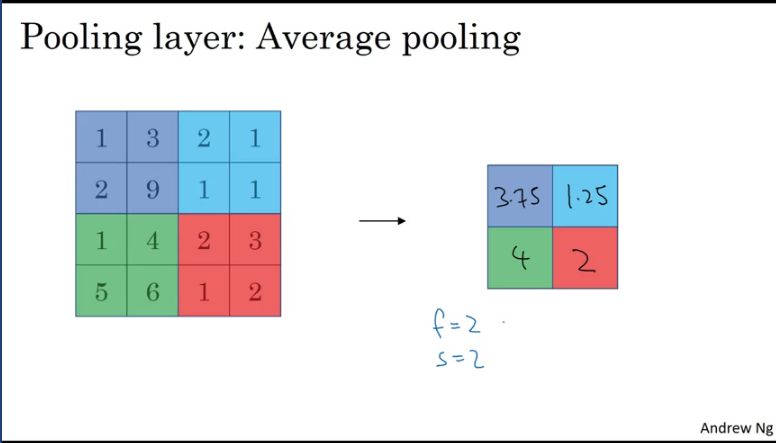
Another type of pooling that isn't used often is the Average pooling. It takes the average of the kernel region.
CNN Example
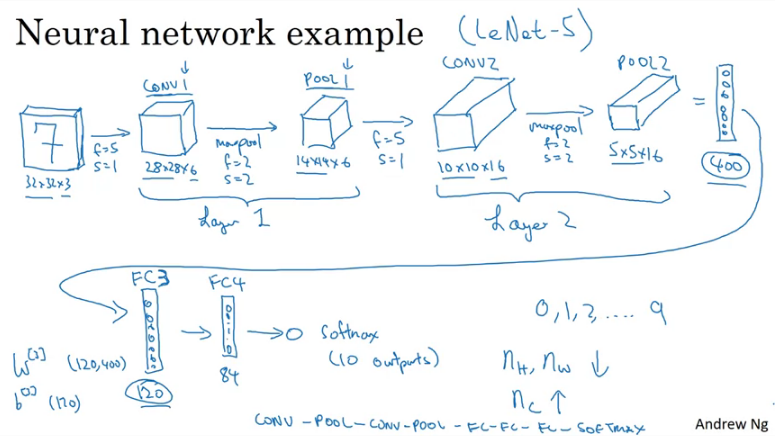
Suppose you are building a hand written digit recognizer as illustrated in the image above. The input image being , the first layer ises a 5x5 filter and string of 1. Then output becomes 28*28*6 if using 6 filters this would form part of layer 1 conv1, next we apply a maxpool (2 filter, 2 stride) this reduces the outut to 14*14*6 and this forms part of layer 1 pool 1 ...So on and so on until you get a flattened pool2 into a 400 dims vector, then build a fully connected layer of 120 nodes (each of the 400 units connect to each of the 120 units)...
The pattern above is very common when working with convnets.
where: Conv→Pool→Conv→Pool→FC→FC→Softmax
Neural network example
| Name | Activation shape | Activation Size | # Parameters |
|---|---|---|---|
| Input | (32,32,3) | 3072 | 0 |
| CONV1 (f=5, s=1) | (28,28,8) | 6272 | 608 |
| POOL1 | (14,14,8) | 1568 | 0 |
| CONV2(f=5,s=1) | (10,10,16) | 1600 | 3216 |
| POOL2 | (5,5,16) | 400 | 0 |
| FC3 | (120,1) | 120 | 48120 |
| FC4 | (84,1) | 84 | 10164 |
| Softmax | (10,1) | 10 | 850 |
In summary, what we see is that the activation size gradually descreases and the pooling layers never have any parameters. Notice that conv later tend to have few parameters. Infact a lot of the parameters tend to be in the fully connected layer of the nn. If the activation size drops too quickly thats usually not great for perfomance.
Why Convolutions?
Why not use fully connected layers, one of the main reason is that if we flatten the input and connect all the neurons to the following layer this would be a lot of parameters to train. The higher the image dimensions the higher the features to train.
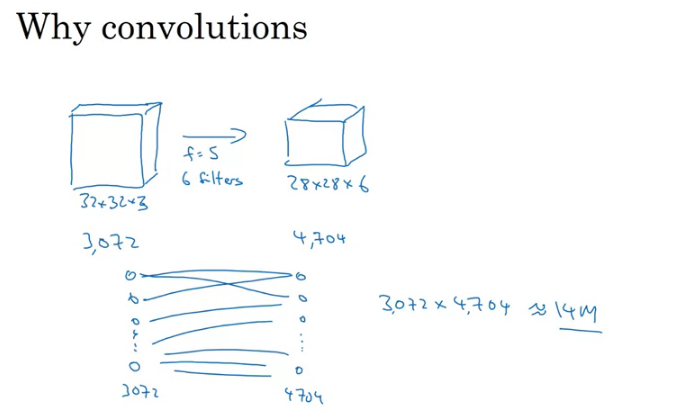
There's 2 main advantages of using convnets over fully connected layers:
- Parameter sharing: A feature detector (such as a vertical edge detector) that's useful in one part of the image is probably useful in another part of the image.
- Sparsity of connections: In each layer, each output value depends only on a small number of inputs.
Putting it all together, suppose you want to create a cat detector as shown in the image below
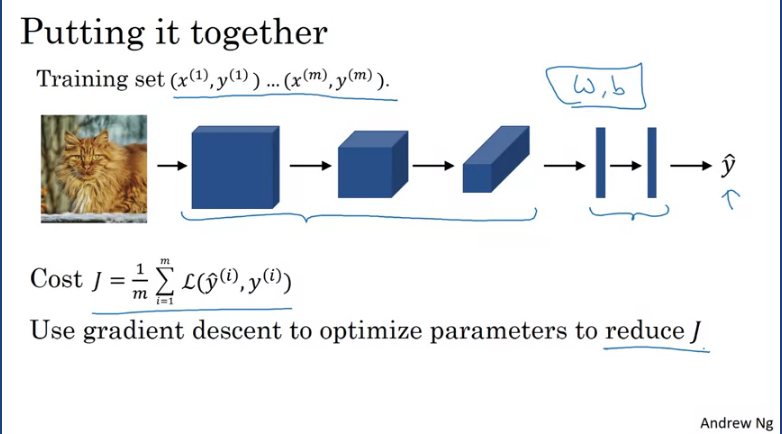
where now, X is an image. And the y's can be binary labels, or one of K classes. And let's say you've chosen a convolutional neural network structure, may be inserted the image and then having neural convolutional and pooling layers and then some fully connected layers followed by a softmax output that then operates . The conv layers and the fully connected layers will have various parameters, W, as well as bias's B. And so, any setting of the parameters, therefore, lets you define a cost function similar to what we have seen in the previous courses, where we've randomly initialized parameters W and B. You can compute the cause J, as the sum of losses of the neural networks predictions on your entire training set, maybe divide it by M. So, to train this neural network, all you need to do is then use gradient descents or some of the algorithm like, gradient descent momentum, or RMSProp or Adam, or something else, in order to optimize all the parameters of the neural network to try to reduce the cost function J.
Resource:
 https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
Q & A
The basics of ConvNets
- What do you think applying this filter to a grayscale image will do?
0 1 -1 0 1 3 -3 -1 1 3 -3 -1 0 1 -1 0
- Detect Vertical edges
- Suppose your input is a 300 by 300 color (RGB) image, and you are not using a convolutional network. If the first hidden layer has 100 neurons, each one fully connected to the input, how many parameters does this hidden layer have (including the bias parameters)?
- 27,000,100
- Suppose your input is a 300 by 300 color (RGB) image, and you use a convolutional layer with 100 filters that are each 5x5. How many parameters does this hidden layer have (including the bias parameters)?
- 2600
- You have an input volume that is 63x63x16, and convolve it with 32 filters that are each 7x7, using a stride of 2 and no padding. What is the output volume?
- 29x29x32
- You have an input volume that is 15x15x8, and pad it using “pad=2.” What is the dimension of the resulting volume (after padding)?
- 19x19x8
- You have an input volume that is 63x63x16, and convolve it with 32 filters that are each 7x7, and stride of 1. You want to use a “same” convolution. What is the padding?
- 3
- You have an input volume that is 32x32x16, and apply max pooling with a stride of 2 and a filter size of 2. What is the output volume?
- 16x16x16
- Because pooling layers do not have parameters, they do not affect the backpropagation (derivatives) calculation.
- False
- In lecture we talked about “parameter sharing” as a benefit of using convolutional networks. Which of the following statements about parameter sharing in ConvNets are true? (Check all that apply.)
- It reduces the total number of parameters, thus reducing overfitting.
- It allows a feature detector to be used in multiple locations throughout the whole input image/input volume.
- In lecture we talked about “sparsity of connections” as a benefit of using convolutional layers. What does this mean?
- Each activation in the next layer depends on only a small number of activations from the previous layer.