Week 4
| Class | C1W4 |
|---|---|
| Created | |
| Materials | https://www.coursera.org/learn/neural-networks-deep-learning/home/week/4 |
| Property | |
| Reviewed | |
| Type | Section |
Deep Neural Network
Deep L-layer neural network
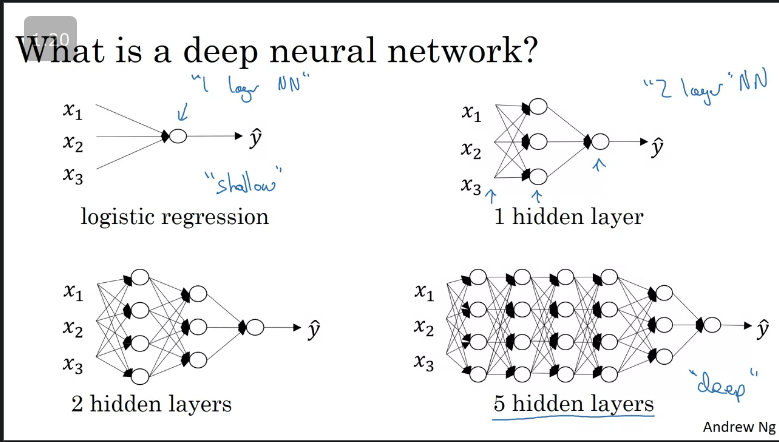
What is a deep neural network?
The image below shows the types of neural network, and we call a logistic regression a shallow neural network and a 5+ hidden layer is a deep neural network.
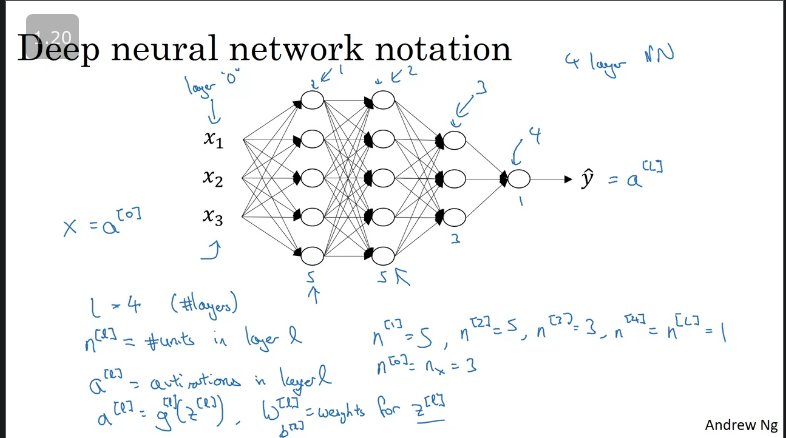
Deep neaural network notation
Below is an image illustrating the notation we use to describe the number of hidden layers denotated by , where is the number of units in layer and is the number of layers.
The neural network below consists of 4 layers and 3 hidden layers, with 3 inputs and 1 output.
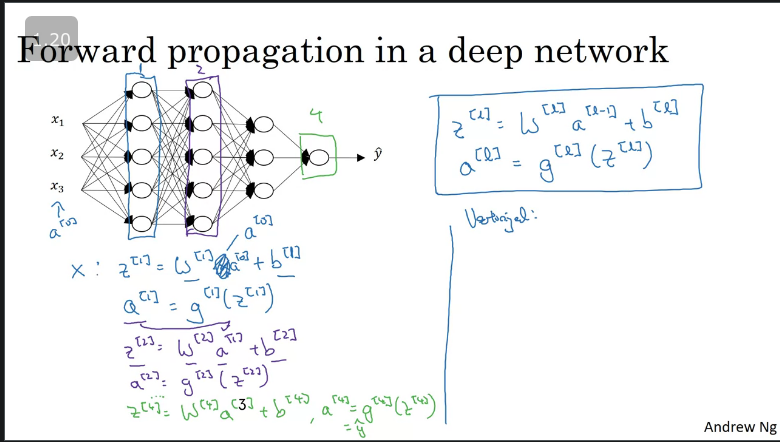
Forward Propagation in a Deep Network
The general forward prop calculation is denoted as:
,
Where is the activations of the output and,
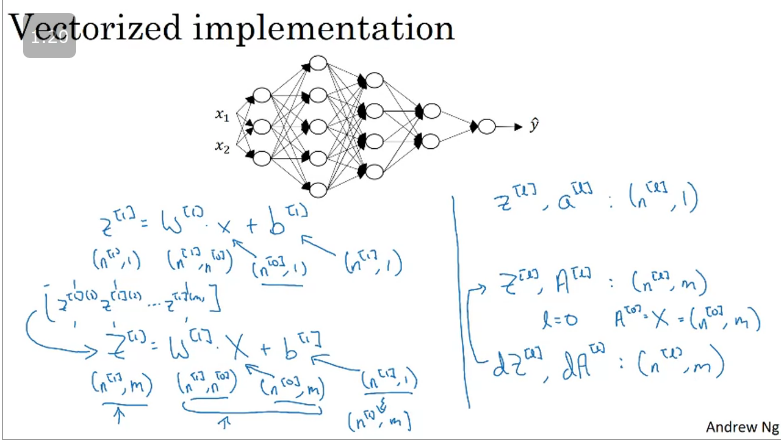
Vectorization
for
Our notation allows us to replace lowercase and with and and that will output the vectorized version. When implementing vectorization you will need an explicit for loop, currently there isn't any way around it.
When working with Deep Neural Networks one should always take note of the shape of matrix they are working with.
Getting your matrix dimensions right
The general formula to check is that when youre implementing the matrix for layer , that the dimension of that matrix be:
Therefore:
=
Note that "a" and "z have dimensions
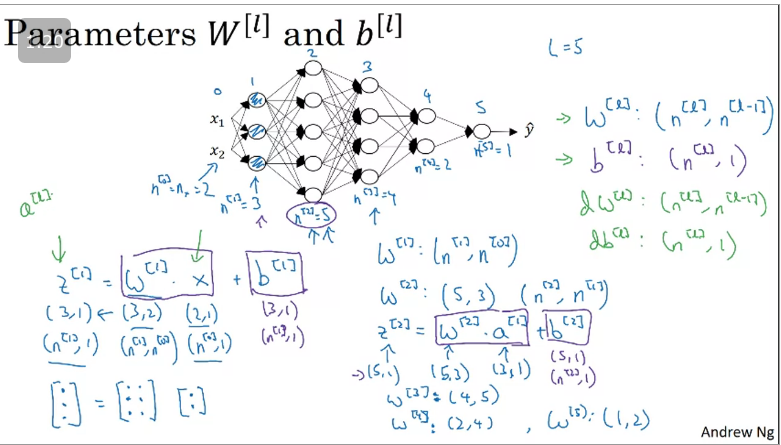
In general, the number of neurons in the previous layer gives us the number of columns of the weight matrix, and the number of neurons in the current layer gives us the number of rows in the weight matrix.
Vectorized implementation
Through Python broadcasting the dimensions for will be broadcasted thus instead of it will be , and will be horizontal matrix and a vertical matrix which will result in being a horizontal matrix.
Why deep representations?
Why deep neural network work well as compared to something else.
Building blocks of deep neural networks
A key takeaway is that, when building a basic building blocks for implementing a deep neural network, in each layer there's a forward propagation step and there's a corresponding backpropagation step as well as a cache to pass the information from one layer to another.
Forward and Backward Propagation
One thing to note is that when computing the output for a forward propagation you'd need an input and cache .
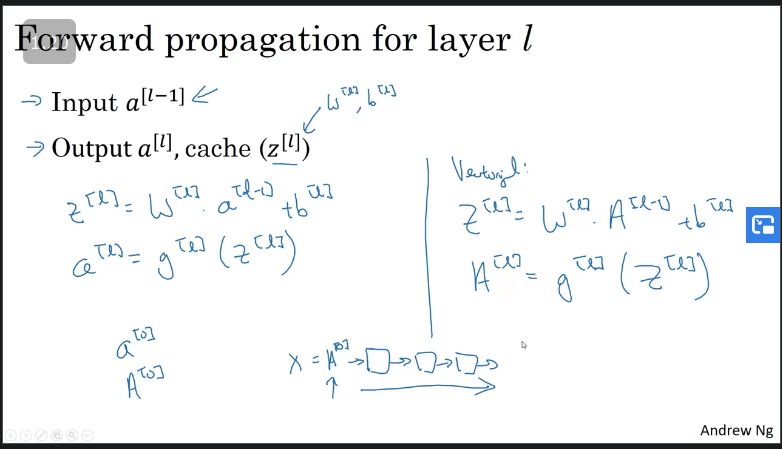
When computing the output for a backward propagation you'd need an input .
Note:

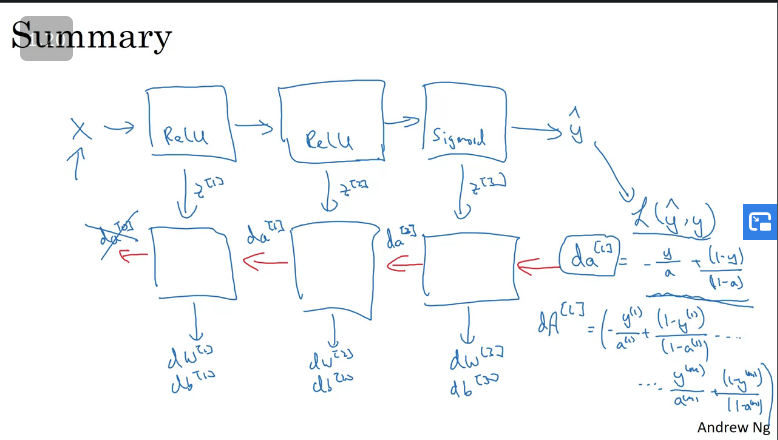
Summary
Suppose you have a 3-layer neural network, which gets initialised with random values of this would compute the value of which you then compute the loss function , while at the same time caching all the values of .
Note that the backward propagation is also initialised to certain values and this is the values of . There is no need to calculate the value of as theres no point in computing the value of the initialisers, hence why it is scratched off in the image.
Parameters vs Hyperparameters
Hyperparameters tell how your learning algorithm resolves such as:
- The learning rate (by setting the learning rate this determines the number of iterations when calculating the gradient descent),
- The number of hidden layer
- The number of hidden units
- The choice of activation function to use.
These hyperparameters determine the final value of and .

ALWAYS REMEMBER:
The difference between np.random.rand and np.random.randn
See explaination here: https://stackoverflow.com/a/47241066 Graphical explaination: https://stackoverflow.com/a/56829859
What does this have to do with the brain?
Q & A
- What is the "cache" used for in our implementation of forward propagation and backward propagation?
- We use it to pass variables computed during forward propagation to the
corresponding backward propagation step. It contains useful values for
backward propagation to compute derivatives.
Justification: Correct, the "cache" records values from the forward propagation units and sends it to the backward propagation units because it is needed to compute the chain rule derivatives.
- We use it to pass variables computed during forward propagation to the
corresponding backward propagation step. It contains useful values for
backward propagation to compute derivatives.
- Among the following, which ones are "hyperparameters"?
- number of layers in the neural network
- number of iterations
- learning rate
- size of the hidden layers
- Which of the following statements is true?
- The deeper layers of a neural network are typically computing more complex features of the input than the earlier layers.
- Vectorization allows you to compute forward propagation in an L-layer neural network without an explicit for-loop (or any other explicit iterative loop) over the layers l=1, 2, …,L. False
- Assume we store the values for in an array called layer_dims, as follows: . So layer 1 has four hidden units, layer 2 has 3 hidden units
and so on. Which of the following for-loops will allow you to initialize the parameters for the model?
for i in range(1, len(layer_dims)): parameter['W' + str(i)] = np.random.randn(layer_dims[i], layer_dims[i-1]) * 0.01 parameter['b' + str(i)] = np.random.randn(layer_dims[i], 1) * 0.01
6. Consider the following neural network.
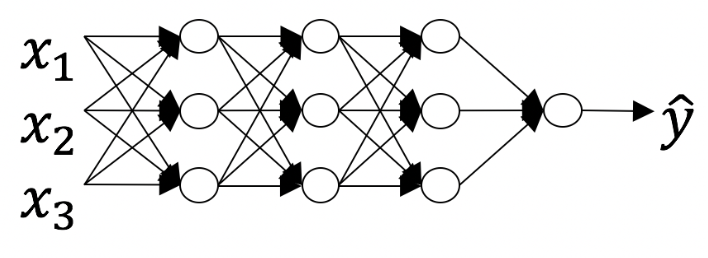
How many layers does this network have?
- The number of layers LLL is 4. The number of hidden layers is 3.
Justification: Yes. As seen in lecture, the number of layers is counted as the number of hidden layers + 1. The input and output layers are not counted as hidden layers.
7. During forward propagation, in the forward function for a layer lll you need to know what is the activation function in a layer (Sigmoid, tanh, ReLU, etc.). During backpropagation, the corresponding backward function also needs to know what is the activation function for layer lll, since the gradient depends on it. True
Justification: Yes, as you've seen in the week 3 each activation has a different derivative. Thus, during backpropagation you need to know which activation was used in the forward propagation to be able to compute the correct derivative.
8. There are certain functions with the following properties: True
- To compute the function using a shallow network circuit, you will need a large network (where we measure size by the number of logic gates in the network), but
- To compute it using a deep network circuit, you need only an exponentially smaller network.
9. Consider the following 2 hidden layer neural network:
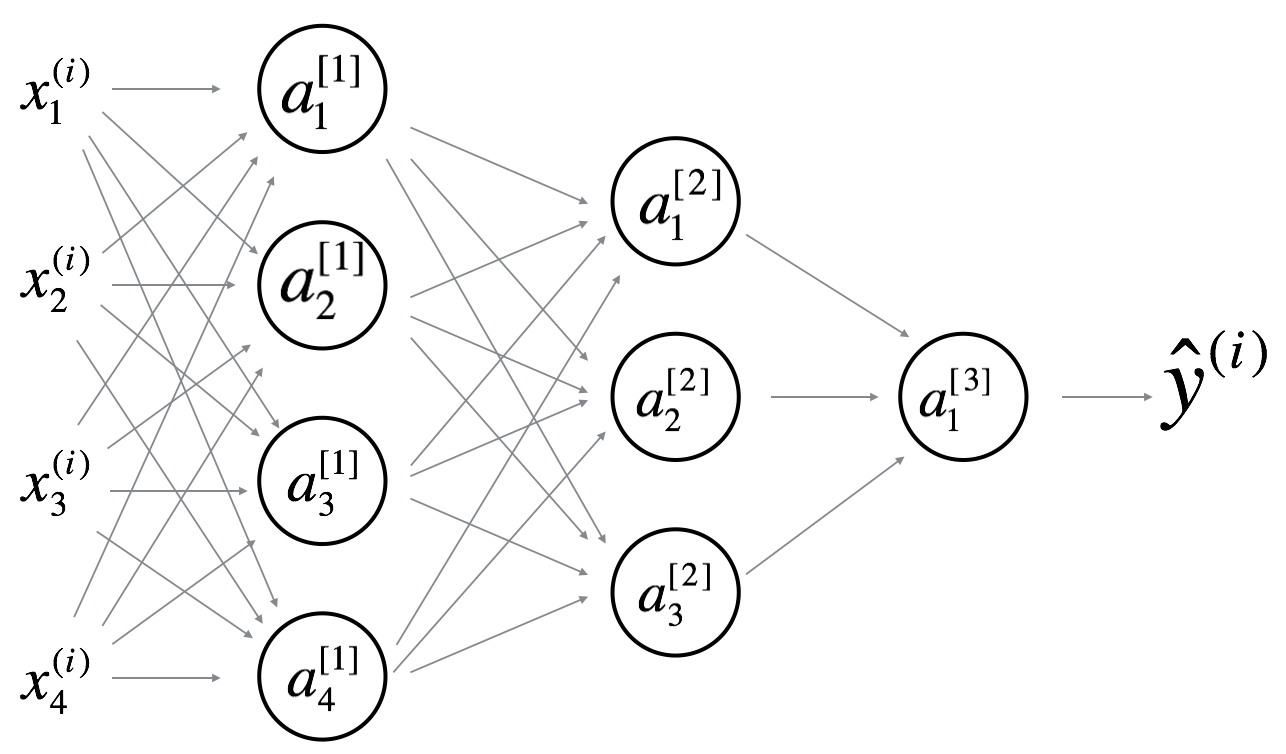
Which of the following statements are True? (Check all that apply).
- will have shape (4, 4)
Justification: Yes. More generally, the shape of .
- will have shape (4, 1)
Yes. More generally, the shape of
- will have shape (3, 4)
Yes. More generally, the shape of
- will have shape (3, 1)
Yes. More generally, the shape of b[l]b^{[l]}b[l] is (n[l],1)(n^{[l]}, 1)(n[l],1).
- will have shape (1, 3)
Yes. More generally, the shape of is .
- will have shape (1, 1)
Yes. More generally, the shape of is .
10. Whereas the previous question used a specific network, in the general case what is the dimension of the weight matrix associated with layer-?
-